Tudo o que você precisa saber sobre triângulos

Triângulo

Região delimitada por três pontos que não estão em uma mesma reta


- Elementos

• vértices: pontos A, B e C.
• Lados: segmentos AB, BC e CA.
• ângulos: BÂC, CBA, ACB.

- Condição de existência

          

          Para que o triangulo ABC exista, é necessário e suficiente que:

• a < b + c
• b < c + a
• c < a + b

- Classificação quanto aos ângulos

I. Acutângulo: todos os ângulos são agudos.

II. Retângulo: Um ângulo reto e dois ângulos agudos.

III. Obtusângulo: Um ângulo obtuso e dois agudos.

- Classificação quanto aos lados

I. Escaleno: Todos os lados são distintos

II. Isósceles: pelo menos dois lados congruentes ( os ângulos opostos aos lados congruentes também são congruentes).

III. Equilátero: os três lados congruentes ( todos os ângulos são iguais a 60°)

Obs.: Um triângulo equilátero é, em particular, isósceles.

Soma dos ângulos internos e Teorema do ângulo externo

I. Soma dos ângulos internos: em qualquer triângulo ABC, vale que  + B + C = 180°.

II. Teorema do ângulo externo: em um triângulo ABC, o ângulo externo é igual à soma dos dois ângulos internos não adjacentes a ele.

- Congruência

I. Definição: dois triângulos são congruentes se possuem lados e ângulos de mesma medida.

II. Caso LLL: todos os lados são congruentes

III. Caso LAL: dois lados congruentes e o ângulo compreendido entre eles também congruente.

IV. Caso ALA: dois ângulos congruentes e o lado compreendido entre eles também congruente.

- Cevianas / Pontos notáveis

I. Cevianas: segmento que une o vértice a um ponto no lado oposto.

II. Mediana - Baricentro

     Mediana: ceviana que une um vértice ao ponto médio do lado oposto.

     Baricentro: ponto de encontro das medianas.

III. Bissetrizes internas - Incentro

      Bissetriz interna: ceviana que divide o ângulo interno em dois outros ângulos iguais.

     Incentro: ponto de encontro das bissetrizes internas

Obs.: O incentro é um ponto equidistante dos lados; assim, é o centro da circunferência inscrita no triângulo.

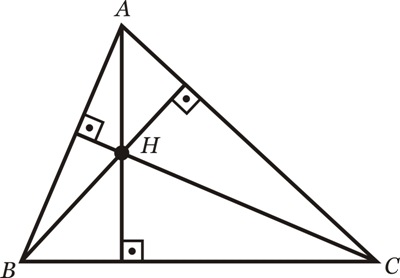
IV. Alturas - Ortocentro

      Altura: ceviana perpendicular ao lado oposto.

      Ortocentro: ponto de encontro das alturas.

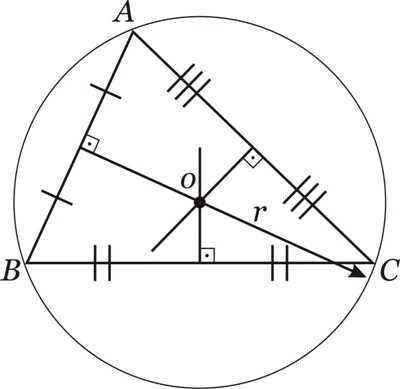
V. Mediatrizes - Circuncentro

     Mediatriz: reta perpendicular ao lado, passando por seu ponto médio ( as mediatrizes não são cevianas).

     Circuncentro: ponto de encontro das mediatrizes.

Obs: O circuncentro é um ponto equidistante dos vértices; assim, é o centro da circunferência circunscrita ao triângulo.

Exercícios:

1) Sejam AÔC BÔC dois ângulos adjacentes tais que AÔB = 2x + 30° e BÔC = 3x - 10. Se AÔC =7x - 40°, determine o valor de x.

2) Seja ABC um triângulo tal que o ângulo  mede 50°. Sendo I o incentro desse triângulo, determine a medida do ângulo BÎC.

Gabarito: 

1) x = 30º

2) BÎC = 115°